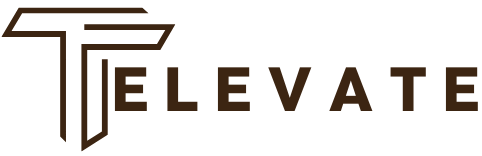The recent design idea (DI) “Negative time-constant and PWM program a versatile ADC front end” disclosed an inventive programmable gain amplifier with integral samples-and-holds. The circuit schematic from the DI appears in Figure 1. Briefly, a PWM signal controls the switches shown. In the X0 positions, a differential signal connected to the inputs of op amps U1a and U1b drives a new voltage sample across capacitor C₁ through switches U2a and U2b. Because switch U2c’s X-to-X1 connection is open, capacitor C₂ is “holding” a version of the previous sample. This “held” version was amplified by the subcircuit consisting of U2a, U2b, U1c, C₁, R₁, R₂, and R₃ with switches in the X1 position. The U1c-based gain-of-two amplifier applies positive feedback through R₁ and U2a to the load of C₁ in series with the resistance of U2b. This causes the voltage across the load to increase exponentially (with a positive time constant), affording a gain which is a function of the time period that the switches are in the X1 position. The advantage of this approach is that programmable, wideband gains of 60 dB or more can be achieved because the op amps’ maximum closed loop gain is only 6 dB; bandwidth is not sacrificed to achieve a high closed-loop gain.

Wow the engineering world with your unique design: Design Ideas Submission Guide

Figure 1 Two generic chips and five passives make a versatile and unconventional ADC front end.

As with any design, this one has errors and characteristics whose nature must be understood before compensation can be considered. These include passive component tolerances; op amp input currents (negligible) and offset voltages; switch turn-on and turn-off times; leakage currents; as well as resistances and switching-induced charge injections. A non-obvious error can also exist which might be termed a “dead zone”. At time t = 0 when the X1 positions are initially active, the sum of a positive low amplitude V_IN – (-V_IN) input voltage sample and various errors can yield a negative voltage at the non-inverting input of U1c. Consequentially, U1c’s output voltage would not trend positive and, assuming the analog-to-digital converter (ADC) driven by V_OUT accepts only positive voltages, the circuit would not work properly. To understand how to bound this undesirable behavior and for other reasons, it’s wise to develop equations to analyze circuit behavior. Some analytic simplicity is possible when the switches are in the X0 position and operation is mostly intuitive. But operation in the X1 position will require a bit of a deeper dive.

Charge injection error

Op amp input offset voltages and switch resistances are commonly well-understood. As for switch leakage current and charge injection, there’s a referenceⁱ that provides an excellent discussion of each. Charge injection Q is most pernicious when the switch transitions from “on” to “off” and a switch terminal is connected to a circuit path which includes a capacitor C and is characterized by a high resistance.

This extends the time for the error voltage Q/C impressed upon the capacitor to “bleed off”. This is not a concern for U2b’s X pin at any time, because both X0 and X1 positions provide a low “on” resistance path. But it must be considered for U2a and U2c when respectively, X0 and X1 turn off. For U2a, X1 is in series with relatively large resistance R₁. When U2c’s X1 is turned off and C₂ is in hold mode (allowing an analog to digital conversion), C₂ sees X1’s multi-megaohm “off” resistance. There is no mechanism to bleed off and recover from U2c’s charge injection error; it is inherent in circuit operation until the PWM reactivates X1 for “tracking” mode, during which time conversions are precluded.

Leakage current

This same high resistance might create a real problem due to leakage current. Such currents flow continuously from U2’s power supplies through its internal ESD diodes to the switch terminals. What saves the circuit from these errors is that an analog to digital (A-to-D) conversion of V_OUT can be triggered quickly after X1 turns off, before significant leakage current errors can accumulate. Leakage from terminal X of U2b can be ignored because as mentioned before, it’s always connected to a low resistance through X1 to ground or X0 to U1b’s output. Not so the X terminal of U2a with its connection to moderately high resistance R₁. Here the leakage current effect must be considered.

LTspice model and equation validation

Taking all this into account, equations can be developed with reference to the circuit seen in Figure 2. Figure 2 is an illustration of the LTspice file developed to model Figure 1 circuit operation and compare it with the equations (which are also evaluated in the file) to ensure their accuracies.

U2a charge injection is not explicitly shown in the circuit, but is incorporated by summing it with the intended input sample voltage Vin in the .param Vc0 statement. The .param statements and the circuit constitute the model. These statements and the algebraic expressions assigned to voltage sources eq_1 and eq_VOUT validate the equations by allowing direct comparisons with the performance of the model. This is accomplished by graphing simulations of the circuit and evaluations of the voltage sources and confirming that eq_1 = e_1 and that eq_Vout = Vout. Not accounted for are switch turn on and turn off times. Their effects will be addressed later.

Figure 2 The LTspice file comparing the performances of the circuit model and the equations developed of it.

Reference Figure 1 and Figure 2, particularly Figure 2’s .param statements. At time t = 0 when the X0 switches turn off and the X1’s turn on, the voltage across C₁ has been initialized to Vc0 as seen in the C₁ initial condition (IC) and the .param Vc0 statements. We can write that the current (w) through C₁ can be seen in [1].

Therefore:

Assuming a solution of the form:    

Where t = time, [3] and [4] can be seen:

And:

Therefore, the voltage at terminal e_1 can be seen in [6].

To evaluate the voltage at terminal e_2 in the model, it is necessary to convolve the signal at e_1 with the impulse response h(t) of the rc and C₂ network shown in [7].

Where the exponential time constant can be seen in [8].

The convolution is given by [9].

This evaluates to [10].

Where:              

Allowing for the U2c charge injection and U1d input offset, shown in [12].

or equivalently:              

The model and this last equation above predict the circuit output at any time t = t₁ immediately after the charge injection of U2c has occurred due to the enabling of the X0 switches.

Assessments

Let’s get some worst-case error parameter values for U1 and U2. The original DI proposed specific op amp TLV9164ⁱⁱ, but not a particular 74HC4053. Surprisingly, there are significant differences between parts from different 74HC4053 manufacturers. The MAX74HC4053Aⁱⁱⁱ looks like a reasonable choice. Let’s consider operation of both IC’s in the commercial temperature range of 0 to 70°C. Refer to Table 1 and Table 2.

Table 1 The TLV9164 maximum parameter values.

Table 2 MAX74HC4053 parameters, maximum values. Note performance degradations when powered by a single supply.

The output of U1c will not move in a positive direction if the sign of the parameter J in [5] is negative. Assuming ADCs whose most negative input value is ground, the circuit will fail to function properly. It’s unlikely that parameters Q1, Voffab, Voffc, and iLeak all take on their worst-case values in a particular circuit, but if they do, Vin will have to be more positive than 10pC/1nF + 2·1.2mV + 1.2mV + 2.5nA * 14300 = 14mV to avoid this “dead zone”. Of course, you’re free to use criterion other than the sum of the worst possibilities, but Caveat Designer!

Another consideration is the circuit settling time in successive PWM periods for the sampling voltage of C₁, particularly in the transit between an ADC full-scale voltage to half of its LSB (this is the most extreme case which might not be a requirement for some applications). For a ±5-V powered MAX74HC4053A, two 125-ohm switches in series drive the 1-nF C₁. With a 12-bit ADC, the required time is (2·125)·1e-9·ln(2¹²⁺¹) = 2.3 µs. Add the switch on-time of 250 ns, and the PWM should enable the X0 switches for t_min = three of its 1 µs cycles for accurate voltage sample acquisition. By comparison, 8-bit ADC’s can get by with 2 µs.

Calibration

The iLeak·R₁ and the temperature-sensitive portions of U1’s input offset voltage errors are negligible in comparison with the ones caused by charge injection. However, as noted in the referenceⁱ and in typical curves provided in the switch datasheetⁱⁱⁱ, the magnitudes and signs of voltages will significantly affect the sizes of the charge injections Q₁ (U2a) and Q₂ (U2c) and also somewhat the ra, rb and rc resistances. For Q₁, ra, and rb, the U1a and U1b input voltages are not determinable from A-to-D conversions. Increasing the values of capacitors C₁ and C₂ will reduce the Q/C charge injection-created error magnitudes but will also necessitate increases in PWM times. Avoiding such time increases by reducing the R₁ value magnifies the errors due to mismatches of ra, rb and rc.

The resistances ra, rb and rc will vary with both temperature and voltage levels. Applying algebra to [13] shows surprisingly that if ra, rb and rc resistances are identical, there is zero error introduced regardless of their value! (This assumes that enough time has elapsed for the e^-t/Tc term to be negligible. ) While not identical, the slightly less than 1% maximum mismatch error can be calibrated out, but only for a given set of switch voltages and temperature. The datasheet does not provide the information required to determine the errors that could occur when the voltages and temperature are other than those present during calibration.

With the circuit as it stands, I know of no way to eliminate temperature- and voltage-sensitive errors. But there are errors insensitive to these conditions that can be calibrated out. The following procedure assumes an ADC of negligible error (its resolution and accuracy require further investigation) and conversion factor CF counts/volt, one perhaps present on the assembly line of a product incorporating this design.

For any instance of this circuit to which specific and accurately known Vin and -Vin (See Figure 1) voltages are applied at a given temperature, [13] can be thought of as a function of time and Vin: V_OUT(t, Vin). V_OUT(t₁, Vin), V_OUT(t₂, Vin), and V_OUT(t₃, Vin) can be captured such that t₃/3 = t₂/2 = t₁ > t_min. A t₁ value of 15 µs is suitable, and Vin = 20 ms avoids the dead zone. (The reason for such a small input voltage is given later.) A t₃ of 45 µs applies a gain of less than 24 and keeps things under a 1.8 V full scale A-to-D level. It will be appreciated that e^t3/T = (e^t1/T)³ and e^t2/T = (e^t1/T)² and that:

where each V_OUT(t, Vin) is scaled by CF to a measurement made by the product line A-to-D. The difference terms cancel the constant terms in [13], and the ratio cancels the A·N term. Such cancellations are necessary if T is to be determined accurately. [14] is a quadratic equation, the desired of the two solutions of which is given by :

From this, the value of T can be obtained (note that T depends slightly on ra because of Req and so it also depends on voltage and temperature):

Further:

Allowing the solution:

N( ) is a function of Vin (see .param N) and is equal to SVin + U where S and U are unknown and again are slightly dependent on the usual. The process of equations [14] to [18] will need to be repeated with a value Vin₂ different from Vin to arrive at an AN₂ term. We could use different values of t, but we might as well keep the same ones. We can safely choose Vin₂ = 25 mV (incurring a charge injection and switch resistances very close to that with Vin = 20 mV) and calculate:

From [13] it can be seen that:

so that:

Given an A-to-D conversion count and reversing [22], it can be seen that:

never forgetting that even this result is influenced by the usual.

Because of their negligible sensitivities to voltage and temperature, NPO/COG capacitors and 25 ppm or better metal film resistors are recommended. 1% or better parts are available at costs around .01 USD in quantity.

Conclusions

This innovative circuit has several features to recommend it. It offers differential to single ended conversion with very high CMRR and wide common mode operating range. It offers gains starting at 6 dB in increments of .6dB limited only by the combination of the sampled voltage and saturation at the positive supply rail. Op-amp gains are no greater than 6 dB, so there is no loss of bandwidth due to operation at high closed-loop gains. But this design has some disadvantages.

A detailed calibration scheme is needed which requires the availability on the production line of an ADC whose requirements for accuracy and resolution have not yet been determined. Even with calibration, various errors which cannot be rescued by calibration can impose an operational “dead zone” for circuit input voltages less than up to 14 mV. Errors due to switch charge injection and switch resistance vary with temperature and applied voltages and are difficult if not impossible to calibrate out. The MAX74HC4053A discussed here is a better ‘4053 than others, but another part may exist with less variations in resistance and charge injection.

I would suggest disconnecting the U2c X0 pin. This connection is of limited usefulness and does damage—it injects charge into U1c, affecting the signal fed through R₁ to C₁. (The effect on C₂ during the “hold” mode can be neglected, being of very short duration due to the X1 rc “on” resistance in the C₂ path.) If it is decided to retain this connection, please note that its effects have not been accounted for in the foregoing analysis.

Finally, I’d like to acknowledge the comments of eldercosta, a review and comments with some unique perspectives by David Lundquist, and especially the comments and contributions of Stephen Woodward, who designed the circuit discussed in this DI.

Christopher Paul has worked in various engineering positions in the communications industry for over 40 years.

References

ⁱ

ⁱⁱ

ⁱⁱⁱ

Related Content

• Negative time-constant and PWM program a versatile ADC front end
• In-situ software calibration of the flying capacitor PGINASH
• Brute force mitigation of PWM Vdd and ground “saturation” errors
• Parsing PWM (DAC) performance: Part 3—PWM Analog Filters
• Minimizing passive PWM ripple filter output impedance: How low can you go?

The post Error assessment and mitigation of an innovative data acquisition front end appeared first on EDN.

Source link